What is Spectral Synthesis?

Spectral synthesis is a lot like wavetable synthesis (of PPG and Waldorf fame) in that it presents a space of harmonically adventurous sounds to scan over, creating unusual timbres. But it actually shares most of its DNA with (frequently misunderstood) additive classics like the Fairlight CMI or Synclavier II. In this post we’ll unpack a bit of that heritage to build up an intuition for what spectral synthesis is and how to use it effectively.

Graphing Sound

Pretty much all the ways we visually represent sounds involve two dimensional graphs. The vertical axis is almost always the same; it represents the loudness of the sound. So it’s what’s across the bottom axis that determines the type of graph we’re looking at.

If we measure time across this horizontal axis, we say we’re in the “time domain”. This gives us wave-like images that look like they might come from an oscilloscope. Fig 1.1 depicts a sine, a square, and a sawtooth wave in the time domain. This is pretty much the default visualization of subtractive synthesis as we know and love it.

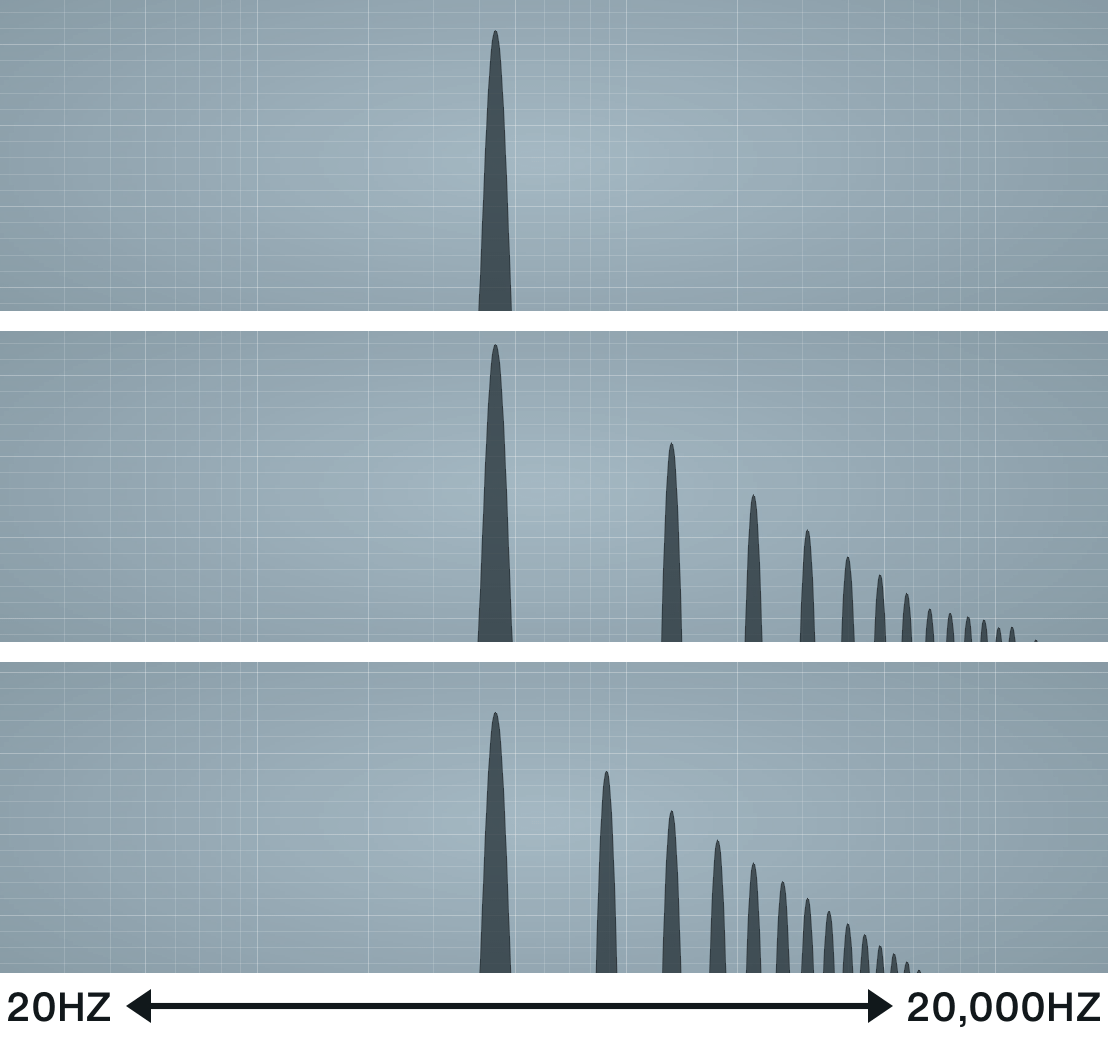
But what if, instead of time, we use that bottom axis to represent frequency? Like, low frequencies on the left and high frequencies on the right? Now we’re in the “frequency domain”, and we get a picture that looks more like what we might see in an equalizer plugin — a sound is broken into its component frequencies, and each is plotted on the graph depending on how loud they are. Fig 1.2 shows the same sine, square, and sawtooth waves, but in the frequency domain.

An interesting thing to notice; the frequencies of these waveforms are discrete — that is, rather than a big hill across the middle of our graph, we see many distinct peaks. Also notable, those peaks all seem to line up with each other. That’s because these sounds are all harmonic, and harmonic sounds are composed exclusively from frequencies from the harmonic series.

A Harmonic Spectrum

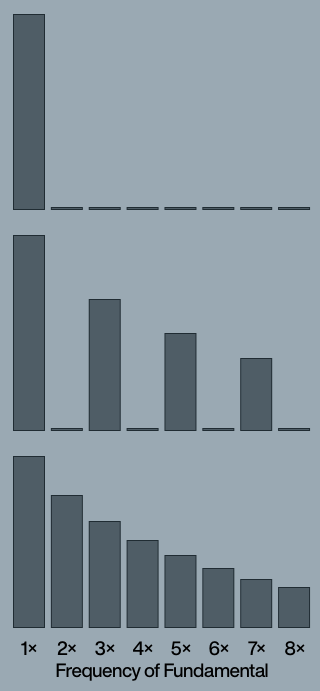
Knowing this, it might occur to us that the frequency domain wastes a lot of space when graphing harmonic content. First, there’s the huge gap in front before we even get to the fundamental. Then there’s a fair bit of space in between each peak that we know we’ll never use because all those frequencies are inharmonic.

So instead of mapping the entire frequency spectrum across our bottom axis, what if we only have the specific frequencies that are part of the harmonic series — a harmonic spectrum? We can make a bar graph where the first bar represents the fundamental frequency (the note we actually play on our keyboard). The next bar represents 2× this fundamental (an octave up). The third is 3× the fundamental (a 5^th further up from that). The fourth, 4× (a 4^th more), then 5× (a major 3^rd up), and so on…

Using this kind of graph to represent the first 8 harmonics of our sine, square, and saw waves would look like fig 2.1. This essentially takes the peaks from the frequency domain in fig 1.2 and turns them into bars. Much tidier! And because this shows harmonic frequencies, and harmonic tones only contain harmonic frequencies, all harmonic sounds can be represented with this type of graph.

Additive Synthesis

So what does all this have to do with spectral synthesis? The key insight is that a “harmonic spectrum” like this isn’t just a way to illustrate harmonic sounds. It can also be used as a recipe to create them. Looking at one of these spectrums, we can see it essentially tells a synth engine how much of which frequencies to play to create a tone.

This is the foundational principle behind additive synthesis. Rather than taking a harmonically rich sound like a saw and subtracting harmonics from it with a filter (as per subtractive synthesis), in additive synthesis we start with a fundamental and then add only the particular harmonics we want by “drawing” them on the graph. The synth then plays back those harmonics with some wave¹ to generate the sound.

The problem with this method is that, as opposed to simply setting an oscillator shape and cutoff as we would in a subtractive patch, additive synthesis requires we set a value for each individual harmonic in our graph. The Synclavier allows programming of 24 individual harmonics. The CMI, a whopping 32! And all that just gives us an initial, stationary tone. If we want it to evolve over time at all, we need to set yet another value for each harmonic for it to interpolate to.

As we can imagine, patching this way gets quite tedious. And additive synths have a reputation for being rather fastidious and difficult for just this reason. But don’t fret! Spectral synthesis greatly simplifies things.

Spectral Synthesis

What if, instead of drawing in each individual bar of our harmonic graph, we picked from a list of preset spectrums instead? And what if, instead of defining how each harmonic independently changed over time, we had a set of clever transformation macros that could act as modulation destinations, automating that work for us?

That the idea behind spectral synthesis. Pick a spectrum, pick a wave to play it, and then transform its harmonics by modulating macros over time. That’s it. We get 80% of the benefits of additive synthesis for only 20% of the work.

And that’s what makes it feel so much like wavetable synthesis in use. The selected preset spectrum is like the starting waveform of the table. Transforming it by manipulating macros sounds like scanning over the waves in a table as our sound smoothly changes from one shape to another. Very Microwave.

The big difference is: while this transformation from shape to shape is hard-coded in a wavetable, with spectral synthesis it’s a generated in real time.

So with a wavetable synth, if we want a different sound when sweeping over a table, we have to load a new wavetable. And if what we want doesn’t exist, we have to figure out how to make a new wavetable that does what we want.

With spectral synthesis, on the other hand, the shape of sounds we sweep over is defined by the values of our macros. So if we don’t like it, we just change the values of one or more macros, their modulation amount, their speed, or whatever. We can hone in on the sweep we want little by little by nudging values.

Thus spectral synthesis not only provides nearly infinite paths through a broad field of wave shapes. It also gives us control over refining and directing that path using the tools of traditional sound design; nudging a knob, listening to the difference, and deciding if we like it.

“But what do the macros do?”

As to the specific functions of these macros, I’m being intentionally vague. Of the spectral engines I’ve used, no two macros do the same thing, so it’s a bit like the wild west out there. Still, there does seem to be a general set of principles all abide by:

• The macro must result in a new spectrum.
  We can imagine a “low pass” macro that progressively mutes lower and lower harmonics until nothing is left. But that doesn’t result in a new spectrum. That results in silence. And silence is a bad thing to sweep through.

  Compare this to the Manatee’s “formant” or CMI V’s “center” macro, each of which can shift existing harmonics to the left, darkening the sound but leaving some sort of spectrum behind (for the next macro to transform!)

• The macro must work for all spectrums.
  Similarly, imagine a “high boost” macro that multiplies the upper harmonics of a spectrum. If our spectrum only has it’s lower harmonics filled in, this macro would have no effect on our sound. Again, “no audible effect” is a bad thing to sweep over.

  Compare with the Manatee’s “inversion” macro, which takes tall harmonics and makes them short while making short harmonics tall. In our example, this would shrink our low harmonics while growing the high ones, having a very audible effect on our sound.

• The macro must be continuous.
  Small changes in macro values must result in small changes to the spectrum. This is what makes sweeping a macro sound like a continuous shifting shape.

  But it’s also what makes tweaking a macro feel natural in the course of sound design. Making a big change, then smaller and smaller ones is what lets us refine our sound. It’s what makes the digital feel analog.

• The result is always harmonic.
  This has less to do with the macros and more with the nature of the harmonic spectrum. Given that each bar in our spectrum represents a harmonic overtone and our transformations can only add or subtract values from these bars, the generated sound is always going to be harmonic.

  As a result, the zone of sweet spots to be found while messing with macros is pretty broad. It’s possible to get crazy, ultra glitchy, and even harsh, but usually in a musical way.

Further Experiments

To play around with a very basic implementation these concepts on your own, you can check out the “Spectral Synth” mode of Arturia’s CMI V (there’s a free demo on their site).

The Manatee by Fred’s Lab has a more robust implementation of these ideas, though. Being hardware, it’s expensive… and can be hard to find at the moment, to boot. But I’ll be posting my experiences with it, so maybe check that out?

Finally, the aforementioned “Spectral Synth” mode is just one small part of the sprawling CMI V plugin. The rest is a very fully featured and accurate recreation of an additive legend. The same goes for Artruia’s Synclavier V plugin, too. If curious to play around with additive synthesis, you cannot go wrong with these two dream machines.